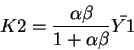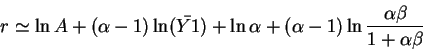Next: About this document ...
CLASS #10: THE INTEREST RATE IN A CLOSED ECONOMY WITH PRODUCTION
From last class, we learned that there exists an interest rate such that
Savings = Investment
- what does the equilibrium interest rate depend upon?
- what does investment in equilibrium depend upon?
In order to address these questions, we will focus on a model with complete depreciation
(simple to solve): capital disappears from one period to the other ( ). Therefore
). Therefore
Investment = Capital Stock.
Since the "social planner"'s equilibrium and the "market"'s equilibrium are
the same, we are going to solve the first one (because it is easier).
Assuming logarithmic utility, and Cobb-Douglas production function,
the planner's problem is:
subject to the constraints:
K2+C1=Y1
and
We know from last time that the FOC deliver the relationship MRS = MRT:
which implies
Using
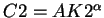 and K2=Y1-C1 we obtain:
and K2=Y1-C1 we obtain:
and
Implications of the above formula: the household invests a fraction
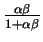 of the available resources, and consumes the remainder.
of the available resources, and consumes the remainder.
The formula says that:
- Investment is pro-cyclical
- The fraction of resources invested depends positively on:
- the share of capital in the production function
 .
What is the intuition?
.
What is the intuition?
- the time discount
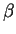 .
What is the intuition?
.
What is the intuition?
The equilibrium (real) interest rate
As we learned in the previous class, in equilibrium the interest rate is determined by the relationship:
(we are using the fact that the planner's equilibrium and the market
equilibrium are the same)
In this specific model:
Since
 ,
then the interest rate is given by the formula:
,
then the interest rate is given by the formula:
How does the equilibrium real interest rate changes with:
- technology shocks (A)?
- the available amount of resources (Y1)?
- the share of capital in the production function
 ?
?
take logs:
The real interest rate:
- increases with a positive technology shock
- low during booms, high during recessions
- increases with

Investment and the Government
Introduce the government in the model, assuming for simplicity that the government spends
an amount of resources G1 in period 1 only. The planner's problem is now:
subject to the constraints:
K2+C1=Y1-G1
and
How do we solve this model? Call
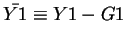 .
The problem is exactly the same one studied above.
The solution is:
.
The problem is exactly the same one studied above.
The solution is:
What happens to Investment? and to the interest rate?
investment decreases: Crowding Out.
Intuition? Permanent income: if your resources today decline because of government spending, you do not want
to reduce your consumption today only, but also your consumption tomorrow. So you reduce your investment.
The interest rate increases. Why? In the graph seen in the last class, the supply of savings is shifting to the left.
The demand for investment by the firm is unchanged. As a consequence, the interest rate increases.



Next: About this document ...
Marco Del Negro
2000-02-08
![]() ). Therefore
). Therefore
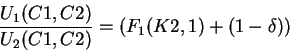
![]() and K2=Y1-C1 we obtain:
and K2=Y1-C1 we obtain:
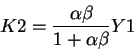
![]() of the available resources, and consumes the remainder.
of the available resources, and consumes the remainder.
![]() ,
then the interest rate is given by the formula:
,
then the interest rate is given by the formula:
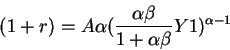
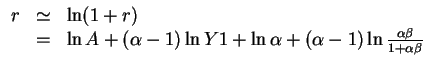
![]() .
The problem is exactly the same one studied above.
The solution is:
.
The problem is exactly the same one studied above.
The solution is: