CLASS #17: THE CONVERGENCE CONTROVERSY

• The Solow growth model predicts convergence toward a steady state.
• This class investigates convergence (unconditional and conditional) and the empirical evidence regarding the neoclassical growth model.

Convergence: the empirical evidence.

Recall that the Solow growth model with capital accumulation predicted:

• If two countries share the same technology (A and $\alpha$), depreciation rate, population growth rate, and saving rate, the steady state will have to be the same: in the long run, the two countries will have the same levels of per capita income, no matter how rich or poor they currently are.
• As a consequence, it must be that countries that are now poor must be growing faster than countries that are now rich (this must be the case if they have to catch up!).
• How well does the model do empirically?

The convergence debate

• Unconditional convergence: assume that all the countries in our sample really share the same technology, saving rate, etc., that is, all countries have the same steady state.
  The prediction is that per capita output must converge.
  The model seems to fare well in:
  • US States, regions
  • European regions
  • OECD countries (selection bias?)
  • not well when the sample includes -almost- all countries in the world.

One may be tempted to conclude that the neoclassical model fares well when the production function is likely to be similar (US States, European regions), or when differences in the steady states are taken into account; but...let us have a closer look at the neoclassical model:
With a Cobb-Douglas production function the growth rate is:

$$\ln{y_{t+1}}-\ln{y_t}=\alpha(\ln{k_{t+1}}-\ln{k_t})+\ln{A_{t+1}}-\ln{A_t}$$

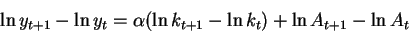
where $A_t=A E_t^{1-\alpha}$
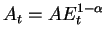
(Note that with technological progress the equation looks the same with:

$$\ln{A_{t+1}}-\ln{A_t}=(1-\alpha) (\ln{E_{t+1}}-\ln{E_t}) \simeq (1-\alpha) \gamma)$$

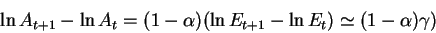
We know that per capita capital evolves as:

$$k_{t+1}=\frac{(1-\delta)k_t+sy_t}{1+\lambda}$$

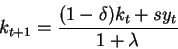
which implies that capital grows approximately at a rate:

$$\ln{k_{t+1}}-\ln{k_t}\simeq sA_tk_t^{\alpha-1}-\lambda-\delta$$

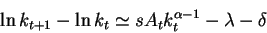
Therefore output grows approximately at the rate:

$$\ln{y_{t+1}}-\ln{y_t} \simeq \alpha s Ak_t^{\alpha-1}-\alpha(\lambda+\delta) +\ln{A_{t+1}}-\ln{A_t}$$

$$=sMPK-\alpha(\lambda+\delta)+\ln{A_{t+1}}-\ln{A_t}$$

$$=\alpha s A^{\frac{1}{\alpha}}y_t^{-\frac{1-\alpha}{\alpha}} -\alpha(\lambda+\delta)+\ln{A_{t+1}}-\ln{A_t}$$

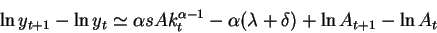
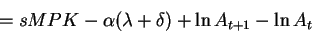
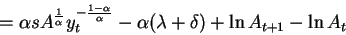
where the last relationship comes from $k_t=(\frac{y_t}{A_t})^{\frac{1}{\alpha}}$

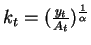
• In 1880 per capita income in the southern states of the US was 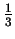$\frac{% 1}{3}$ of income in the north. With 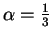$\alpha=\frac{1}{3}$, this implies that the marginal productivity of capital in the south was about 10 times higher than in the north. With $\alpha=.4$, about 3 times higher.
  Notice in fact that:
  
  $$MPK=\alpha A^{\frac{1}{\alpha}} y_t^{-\frac{1-\alpha}{\alpha}}$$
  
  
  if y_tⁱ=qy_t^j then
  
  $$MPK^i=MPK^jq^{-\frac{1-\alpha}{\alpha}}$$
  
  
  This observation raises two questions (Romer 1994):
  • Why did they take so long to converge? the estimated rate of convergence (2%) is much lower than the one implied by these income differences.
  • How can MPK's be so different within the same country? what sort of barriers to capital mobility could justify these differences?
• In 1960 per capita output in the Philippine was about 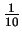$\frac{1}{10}$ of per capita output in the US, yet the US and the Philippine grew roughly at the same rate in the last 40 years. Can the neoclassical growth model handle this evidence without invoking differences in technology?
  Remember:
  
  $$\ln{y_{t+1}}-\ln{y_t}\simeq sMPK-\alpha(\lambda+\delta)+\ln{A_{t+1}}-\ln{A_t}$$
  
  
  • This difference in per capita income implies that the MPK in the Philippine is 100 times larger than in the US. For the growth rates to be the same, the savings rate in the US must have been 100 times larger. Or the growth rate in population x00's times lower. very implausible!

How can the neoclassical model be rescued? Two avenues:

• Admit that technology evolves differently across countries (Barro and Sala-i-Martin): ``diffusion of technology'', conditional convergence.
• Introduce human capital in the model (Mankiw, Romer, Weil; 1992)

First avenue: conditional convergence.

Conditional convergence: admit that countries have different technology parameters, that is, have different steady states (remember: different saving rates or population growth are not much help). Conditional on the steady state, the model still predict that countries that are further away from their own steady state should grow faster. How do you condition? have in your regression variables that affect technology (openness to trade, degree of development in financial markets, level of education, the size of the government, etc.). The model fares well also when the sample includes -almost- all countries in the world.
Note that with differences in technology the MPK's across countries (states) can be the same even if per capita output is very different.

Second avenue: human capital.

Assume that the production function is also a function of human capital:

$$Y_t=A_tK_t^{\alpha}H_t^{\alpha}N_t^{1-2\alpha}$$

where H is human capital, or

$$y_t=A_tk_t^{\alpha}h_t^{\alpha}$$

where k and h are respectively physical and human capital per worker. This means that per capita output growth is:

$$\ln{y_{t+1}}-\ln{y_t}=$$

$$=\alpha(\ln{k_{t+1}}-\ln{k_t})+ +\alpha(\ln{h_{t+1}}-\ln{h_t})+\ln{A_{t+1}}-\ln{A_t}$$

Assume that human capital and physical capital are proportional, ie, countries with a lot of physical capital also have a lot of human capital:

h_t=bk_t

,where b is the amount of resources invested in human capital as fraction of investment in physical capital.
Substitute for h in the production function and obtain:

$$y_{t}=A_{t}k_{t}^{2\alpha }b^{\alpha }$$

It can be shown formally that the effect of introducing human capital (and the proportionality assumption) is like doubling the coefficient on capital,i.e., mitigating the effect of decreasing returns to capital. Remember from before:
if y_tⁱ=qy_t^j then $MPK^{i}=MPK^{j}q^{-\frac{1-\alpha }{\alpha }}$
but now we have:
if y_tⁱ=qy_t^j then $MPK^{i}=MPK^{j}q^{-\frac{1-2\alpha }{2\alpha }}$
So the difference in per capita income between US and Philippine implies that the MPK in the Philippine is only roughly 3 times larger than in the US. So for the growth rates to be the same, the savings rate in the US must have been only 3 times larger, which is a plausible number. Yet, why does not human capital migrate from the countries where it is abundant to those where it is scarce?
You can compute that the returns to human capital are at least twice as high in the Philippine than in the US: why do people with human capital not migrate to the Philippine?

What do we conclude?

• Convergence or Not Convergence? The evidence is mixed.
• The Solow growth model does not fit reality perfectly well, and leaves many questions unanswered. ..
• at the same time, it also seems to have some empirical appeal. It should not be discarded too quickly.