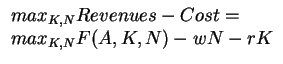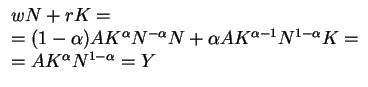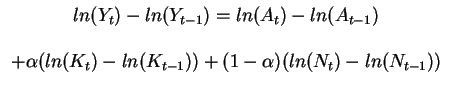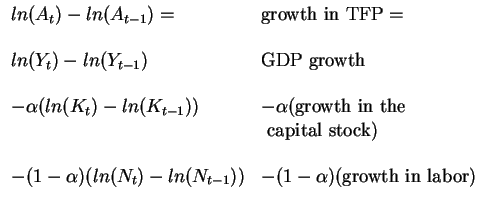Next: About this document ...
CLASS #8: PRODUCTION: THE PRODUCTION FUNCTION
Ch. 3
- Move away from "endowment economy" where output was treated as given
(fruits from tree)
- Understand the determinants of output: capital, labor, and
productivity
Introduce a production function that depends on the inputs:
capital and labor
Y=F(A,K,L)
where Y is output, K is capital, N is labor, and A is
"total factor productivity"
total factor productivity: how K and N are "mixed" together in
order to produce Y (example: cooking)
we will often focus on a Cobb-Douglas production function:
nice properties of Cobb-Douglas
- increasing in both capital and labor; need both in order to produce
- if you double the inputs, the output doubles
- decreasing marginal returns to capital and labor
- product exhaustion
- constant factor shares
Increasing in both capital and labor
need both in order to produce
Homogeneity of degree one
with twice as much capital and twice as much labor one obtains
twice as much output, for given productivity (like recipes)
Decreasing marginal returns to labor and capital
Adding one more worker, for a fixed amount of capital,
will increase production by less and less the larger the number of workers
that are already operating the machines
Define MPN = marginal productivity of labor, as
The marginal productivity of labor is an increasing function of the
capital/labor ratio
Likewise, adding one more unit of capital, for a fixed amount of
labor, will increase production by less and less the more capital you
already have in place.
Define MPK = marginal productivity of capital, as
The marginal productivity of capital is a decreasing function of the
capital/labor ratio.
Aside: How are the remunerations (wages and return to capital)
of the two inputs (labor and capital) determined in a competitive economy?
Let us study the problem of a firm that hires labor at the market wage w
and rents capital at the market interest rate r.
As we are in a competitive environment, the firm takes the cost of both labor and
capital as given, and chooses the amount of labor to hire and capital
to rent with the goal of maximizing profits:
As a result:
Product Exhaustion
The remuneration of capital and labor exhausts all production Y
- when prices are competitively determined
(all production functions that are homogeneous of degree one)
Profits are zero
Constant factor shares
What is the fraction of GDP which is to pay labor? and capital? (when
prices are competitively determined)
so factor shares are constant over time, which is what has been observed
from the (US) data
Since the factor share for labor and capital are respectively 2/3 and 1/3,
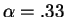 seems to be a good guess
seems to be a good guess
What is capital and what is labor?
HUMAN CAPITAL
- Education
- Learning how to operate a machine
This is a very important issue for policy: how much should a country invest
in physical capital, and in education?
Including human capital,
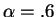 may be a better guess
Do "real world" data satisfy this equation with
may be a better guess
Do "real world" data satisfy this equation with
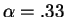 ?
?
Notice that per capita output (y) is equal to:
and the capital to output ratio (k):
or
from which we obtain:
taking logarithms we get:
if this relationship holds for each country, it should hold for the world as
a whole:
taking differences (assuming A is the same for all countries):
if
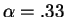 ,
then
,
then
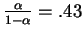 .
For Switzerland,
.
For Switzerland,
 ,
and therefore we should have
,
and therefore we should have
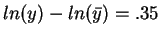 ( if the
capital/output ratio is 81 % larger then the world average, per capita
output should be 35 % larger ).
( if the
capital/output ratio is 81 % larger then the world average, per capita
output should be 35 % larger ).
For Ethiopia,
 ,
and
therefore we should have
,
and
therefore we should have
 ( if the world average
capital/output ratio is 108 % larger than Ethiopia's, the world average per
capita output should be 46 % larger than Ethiopia's).
( if the world average
capital/output ratio is 108 % larger than Ethiopia's, the world average per
capita output should be 46 % larger than Ethiopia's).
In fact, for Switzerland per capita output is 153 % larger, and for Ethiopia it is 221% smaller.
With
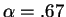 we are closer to reality. (evidence from Chari,
Kehoe, McGrattan, 1997, and George Hall)
we are closer to reality. (evidence from Chari,
Kehoe, McGrattan, 1997, and George Hall)
Total Factor Productivity (TFP or "Solow Residual")
The part of growth in output that is not explained by growth in the two
inputs, labor and capital.
If we take the logs of the production function:
at time t and t-1 and subtract
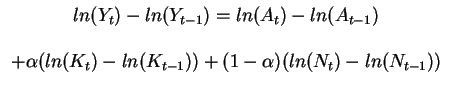



Next: About this document ...
Marco Del Negro
2000-02-02