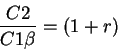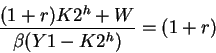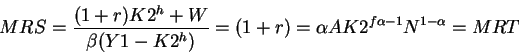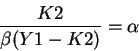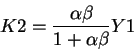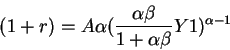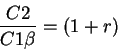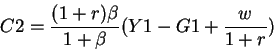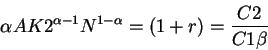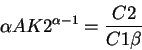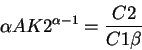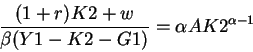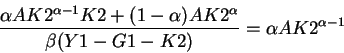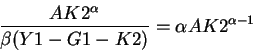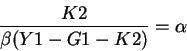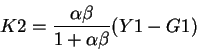Next: About this document ...
Economia V; Instructor: Marco Del Negro
Problem set 5
Solutions
1A) The problem of the consumer is:
s.t.
Y1=K2+C1
C2=(1+r)K2+ W
The householdīs budget constraint can be rewritten as:
1B) the problem of the firm is:
Max K2,N F(K2,N)-(1+r)K2-WN
1C) To find the equilibrium in the decentralized economy we have to solve the consumer's problem,
the firm's problem, and then impose the equilibrium condition that savings by the household is equal to the investment
by the firm. The first order condition for the consumer's problem is, as we saw in class:
From the budget constraints of the household we have: C1=Y1-K2 and
C2=(1+r)K2+W. Substituting these expressions into
the first order condition we obtain a relationship between the desired K2 of the household (K2h) and the
interest rate:
The first order conditions for the firm, as we saw in class, are:
The first FOC determines a relationship between the desired K2 of the firm (K2f) and the
interest rate:
Note that the right hand sides of the two FOCs (for household and consumer) are the same, so we get:
In equilibrium the amount of capital the household decides do save has to be equal to the amount of capital
the firm wants to invest:
K2h=K2f=K2
where K2 is the equilibrium amount of capital, and the amount of labor the household decides do supply (equal
to 1, by assumption) has to be equal to the amount of labor the firm wants to hire. So N=1, and we have:
Using the fact that
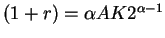 and
and
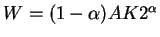 we can rewrite the above relationship
as an equation in only one unknown, K2:
we can rewrite the above relationship
as an equation in only one unknown, K2:
The rest is algebra:
or
which is the same equilibrium found for the decentralized economy.
1D) The answer is: Second Welfare Theorem. The intuition is that in the decentralized economy
the interest rate (the price) adjusts so that the MRT and the MRS are equal, as in the centralized economy.
1F) From the FOC of the firm:
Since
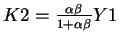 we obtain:
we obtain:
2A) The presence of the government changes the problem of the consumer.
Now the problem of the consumer can be described -in words- as follows. She can use the available amount
of resources (Y1) in three ways: i) consume (C1), ii) invest in capital (K2), iii) invest in government bonds (B2).
If she invests in capital, the next period she will have (1+r)K2. The first period budget constraint is therefore:
Y1=K2+C1+B2
If she invests in government bonds, the next period she will have (1+rg)B2.
So the second period's budget constraint is:
C2=(1+r)K2+ (1+rg)B2+w-T2
where w-T2 is the income she receives in the second period minus taxes. The overall problem is:
s.t.
Y1=K2+C1+B2
C2=(1+r)K2+ (1+rg)B2+w-T2
2B) The problem of the firm is:
Max K2,N F(K2,N)-(1+r)K2-WN
2C) In period 1 the government is collecting no taxes. Therefore must finance all its spending by
borrowing.:
B2=G1
In period 2 the government has to collect taxes in order to pay back what it owes:
T2=(1+rg)B2
Note that the two constraints imply:
T2=(1+rg)G1
2D) The problem of the firm is the same one as before. Its FOC are then:
The problem of the consumer is different. Let us substitute the constraints in the objective function and
rewrite it as:
The FOC with respect to K2 is the same one as before:
While the FOC with respect to B2 is:
Now note that the left hand sides in the two FOCs are the same. Therefore the left hand sides must be the same:
r=rg
This result should be no surprise. It is an arbitrage result: if government bonds and capital yielded different
returns none would invest in either one of these. So in equilibrium they must have the same return.
If this is the case, we can rewrite the budget constraints of the agent as:
Y1=(K2+B2)+C1
C2=(1+r)(K2+B2)+w-T2
Define X as
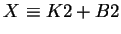 .
Then:
.
Then:
Y1=X+C1
C2=(1+r)X+w-T2
The second budget constraint implies that:
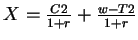 .
Substitute into the first
constraint and obtain:
.
Substitute into the first
constraint and obtain:
Since
T2=(1+r)G1 the above constraint becomes:
Note that we have rewritten the problem of the consumer as follows:
s.t.
But the solution to this problem is well known! As we saw in class:
Here we have the answer to questions 2E and 2F! The equilibrium consumption does not depend
on the timing of taxes, but only on the present value of government spending. So the equilibrium
consumption is the same if T1=G1, and Ricardian equivalence holds. So much for consumption, but what about
capital. Note that from the FOCs of firm and consumer we have:
Imposing N=1 this condition becomes:
The right hand side of this equation depends on C1 and C2. The left hand side depends only on K2.
Since C1 and C2 do not depend on the time pattern of taxes, neither does the left hand side.
But this implies that the right hand side, and therefore K2, does not depend on the time pattern of taxes. Ricardian
equivalence was proven!
To find the equilibrium level of K2 we proceed as above (remembering that in equilibrium
K2h=K2f=K2)
we proceed as above.
becomes (using the budget constraints and the fact that B2=G1 and
T2=(1+r)G1=(1+r)B2)
using the fact that
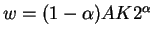 we get:
we get:
or
2E) See above.
2F) See above.



Next: About this document ...
Marco Del Negro
2000-02-22