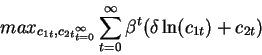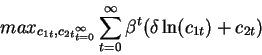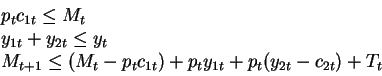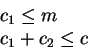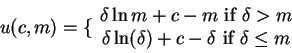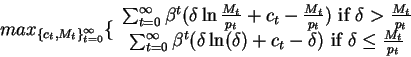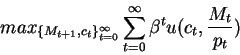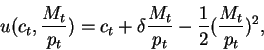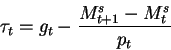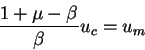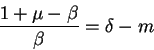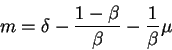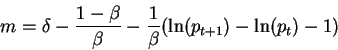Next: About this document ...
TEORIA Y POLITICA MONETARIA, SPRING 2000; INSTRUCTOR: MARCO DEL NEGRO
Midterm Exam, Solutions
1) [15] Explain why, in general, real money balances enter the indirect utility function in
the Sidrauski-Brock model. Assume that the government, all of a sudden, prevents by law the
use of credit cards. Other things being equal (money supply and output) what happens
to real money balances, and the price level?
Real money balances enter the indirect utility function in the Sidrauski-Brock model because,
for a given amount of total consumption c, having real money balances gives the agent a chance to
purchase cash goods. Without real money balances, the agent cannot consume any cash goods, and has to spend all
c on credit goods. If the government, all of a sudden, prevents by law the
use of credit cards, a number of goods that were before considered `credit goods' become `cash goods'.
People would demand more real money balances, as they need them to purchase goods (formally, um would rise,
shifting down the f(m) curve discussed in class). For given money supply, the price level would fall.
2) [15] Express Friedman's rule (the optimal rate of money growth)
and explain it. What would be wrong with a rate of money growth below Friedman's rule ?
Friedman's rule states that monetary authorities should lower the rate of money creation, and therefore the rate of
inflation, until the nominal interest rate
equals zero. Formally,
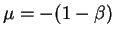 .
By doing so, the monetary authorities would eliminate the opportunity cost
of holding money. Hence individuals will hold as much real money balances as they would like. This in turn eases
their transactions and therefore increases their utility. A rate of money growth below Friedman's rule
implies a negative nominal interest rate. But the nominal interest rate cannot be negative, as it is not
an equilibrium. The equilibrium condition states that:
.
By doing so, the monetary authorities would eliminate the opportunity cost
of holding money. Hence individuals will hold as much real money balances as they would like. This in turn eases
their transactions and therefore increases their utility. A rate of money growth below Friedman's rule
implies a negative nominal interest rate. But the nominal interest rate cannot be negative, as it is not
an equilibrium. The equilibrium condition states that:
Ruc=um
if R is negative the right hand side is negative (uc is always non-negative), but the left hand side cannot be
negative, since um is always non-negative. Money is ``too'' attractive an asset when nominal interest rates are
negative for an equilibrium to exist.
3) [25] The household's problem is:
subject to the constraints:
where Mt+1 is the amount of money held by the households at the end of period t, c1t and
c2t represent the consumption of cash and credit goods respectively in period t, pt is
the price of both goods in terms of money, yt represents the endowment of the household at the beginning
of period t, which can be used to produce both cash goods (y1t) and credit goods (y2t),
and Tt represents nominal transfers from the government.
Solve the intratemporal problem and find the indirect utility function. Write the objective function and the
constraints for the intertemporal problem.
Here you have to solve for the intratemporal problem, which is:
subject to the constraints:
where
 .
Just as in class, you can tackle this problem by forgetting about the `cash-in-advance'
constraint, and solving:
.
Just as in class, you can tackle this problem by forgetting about the `cash-in-advance'
constraint, and solving:
or
The FOC is:
and the solution is:
Of course, this is `the' solution only if it satisfies the `cash-in-advance' constraint. Otherwise, if
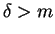 ,
the solution is:
,
the solution is:
c1=m
c2=c-m
(note that the FOC for
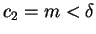 is positive! The agent would like to spend more on c1 if she could).
So the indirect utility function is:
is positive! The agent would like to spend more on c1 if she could).
So the indirect utility function is:
and the intertemporal problem is:
s.t.
4) [35] Consider an economy where the government budget constraint is:
The household solves the problem:
subject to
and
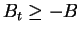 , where B is some positive number.
Assume that the utility function is of the form:
, where B is some positive number.
Assume that the utility function is of the form:
where 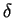 and
and 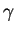 are positive numbers, and that:
are positive numbers, and that:
a) Find equilibrium taxes (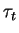 ). Discuss whether Friedman's rule is optimal in this economy.
). Discuss whether Friedman's rule is optimal in this economy.
b) Find equilibrium consumption.
Find the equilibrium real money balances as a function of 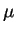 ,
, 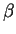 , and
, and 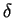 .
Show that the equilibrium real money balances are a decreasing function of
.
Show that the equilibrium real money balances are a decreasing function of 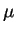 .
.
c) The following is a standard specification of the money demand equation:
Show that you can derive this money demand equation from the model you just solved, and find the
values of 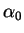 and
and 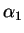 in terms of the parameters
in terms of the parameters 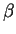 and
and 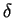 .
.
a) Dividing the budget constraint of the government by the price level one obtains, after imposing the condition
Bst=0:
Since money growth is constant and equal to 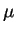 ,
real seignorage is
,
real seignorage is
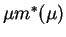 and equilibrium taxes are:
and equilibrium taxes are:
b) Using the individual and the government's budget constraint one obtains equilibrium consumption:
ct=y-g.
The equilibrium condition for real money balances is:
which becomes:
or
which shows that equilibrium real money balances are a decreasing function of 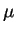 .
.
c) Recognizing that equilibrium inflation is 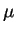 ,
that is:
,
that is:
the above formula becomes:
or
so



Next: About this document ...
Marco Del Negro
2000-03-16