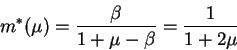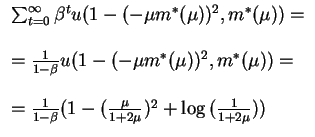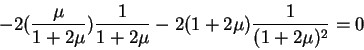Next: About this document ...
Marco Del Negro, Teoria y Politica Monetaria, Spring 2000
Problem set 5
Solutions
a) In order to find the optimal 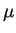 one has to consider the equilibrium conditions. These are the same as
in the last problem set, and are repeated here for convenience. Under the assumption that money supply grows at a
constant rate, seignorage is equal to
one has to consider the equilibrium conditions. These are the same as
in the last problem set, and are repeated here for convenience. Under the assumption that money supply grows at a
constant rate, seignorage is equal to 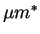 ,
where m* is equilibrium real money balances.
This implies that in all periods:
,
where m* is equilibrium real money balances.
This implies that in all periods:
The first order condition with respect to money are:
where we used the equilibrium condition for ct (that is:
 ).
The expression for
).
The expression for 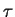 can be substituted in to obtain:
can be substituted in to obtain:
Since uc=1 and
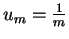 ,
the equation becomes:
,
the equation becomes:
This equation can be solved for its only unknown, m*, thereby obtaining:
Equilibrium consumption is equal to:
b) Once you have found the equilibrium real money balances as a function of 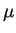 ,
they can be plugged into the
objective function of the household to obtain:
Note that there is a trade-off involved in the choice of
,
they can be plugged into the
objective function of the household to obtain:
Note that there is a trade-off involved in the choice of 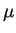 .
A decrease in
.
A decrease in 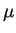 entails an increase in real money balances, and consequently an increase in utility,
but also a decrease in seignorage and an increase in taxes. Since taxes are distortive consumption will decrease.
The first order condition with respect to
entails an increase in real money balances, and consequently an increase in utility,
but also a decrease in seignorage and an increase in taxes. Since taxes are distortive consumption will decrease.
The first order condition with respect to 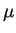 is:
is:
or
or
The two solutions to this equation are -1 and 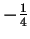 .
We know that Friedman's rule is
.
We know that Friedman's rule is
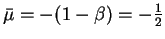 .
Therefore
.
Therefore 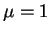 cannot be the solution (why?). So the only solution is
cannot be the solution (why?). So the only solution is
 .
So the optimal rate of inflation is negative, but it is above Friedman's rule. Why? See
next point.
.
So the optimal rate of inflation is negative, but it is above Friedman's rule. Why? See
next point.
c) Since taxes are distortive, the higher the level of
taxes the lower the available amount of resources, and of consumption. Ramsey principle says it is optimal
to equalize marginal distortions. If Friedman's rule is implemented, the distortion on real money balances is zero, and
the distortion due to taxes is positive. Therefore, in this economy Friedman's rule cannot be optimal.



Next: About this document ...
Marco Del Negro
2000-02-19