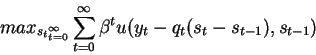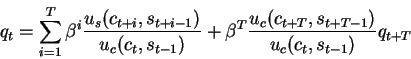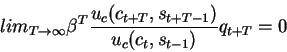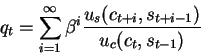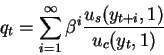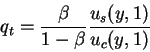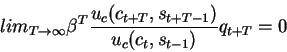Next: About this document ...
CLASS 2: THE PRICE OF DURABLE GOODS
- study how the price of a durable good (refrigerator)
is determined
- emphasize how forward looking behavior (expectations) is -again- crucial in
understanding the determination of the price of a durable good
- this is useful because money shares many features of durable goods
Price of Durable Goods in an Infinite Horizon Model
this model shares a number of assumptions with the previous one. In
particular:
- the economy lasts an infinite number of periods, t=0,1,2,...
- there is a representative household in the economy
- in each period the households receives an amount of income yt
in terms of the consumption good
- the aggregate supply of refrigerators is normalized to 1, and is constant
in all periods. However the household see itself as being able to choose how much
to invest in refrigerators
- at the end of period t the refrigerator is worth qt units
of the consumption good
- in each period the household decides how much to consume,
and how much to invest, that is, how many cows to own
let us denote st the amount of refrigerators owned by the household
at the end of period t (beginning of period t+1)
the main difference is that the durable good does not produce a
dividend in each period, like a stock, but produces a service, in the
sense that it raises the utility of the agent (in a sense, the ``dividend"
from the durable good is in terms of ``utils", not in terms of consumption
good).
the household's problem is:
subject to the budget constraint (which holds in each period t):
the service the household receives in period t from holding the durable
goods are proportional to the amount of durable good held at the
beginning of period t, that is st-1
as before, in equilibrium all these constraints will hold with = sign, so
we can substitute the constraint in the objective function:
Let us focus on the first order condition (FOC) with respect to st
Notice that the term st appears in the sum above only in the two terms:
so the first order condition is:
where
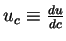 ,
and
,
and
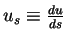 which can be rewritten as:
which can be rewritten as:
following what we did in the previous model,
we can write the FOC for periods
t+1,..,t+T,
substitute again and again for
qt+1 uc(ct+1,st),...
and obtain the following expression:
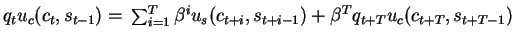 which can be rewritten as:
which can be rewritten as:
What happens to the right hand side of this expression as we let
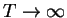 ?
?
as in the previous model, assume for the time being that
,
then we obtain:
the above condition determines the price of a durable good (refrigerator)
and can be interpreted as follows:
- the value of a durable good is a present discounted value of all
future services provided by the good
- the price of the durable good depends on the
marginal rate of substitution (MRS) between consumption of the non
durable good (c) at time t and the services from the durable good
at time t+i.
This suggests that:
- in periods when people consume a lot
of the consumption good (booms) the price of the durable good is
driven up as well: when ct is high, the denominator
uc(ct,st-1) is low
- the value from durable goods depend crucially on the
extent to which the services they provide and consumption of the
non durable good are substitutes or complements
equilibrium
in equilibrium it must be that in each period ct=yt and st=1
the pricing formula then becomes:
in particular, if income is constant over time (yt=y all t),
we obtain that the price of the non durable good is also constant:
we can now discuss why the transversality condition must hold in this model:
- first, notice that is income yt is bounded away from zero
and infinity in all periods (
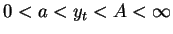 all t), the term
all t), the term
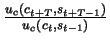 must also be bounded
away from zero and infinity, since ct=yt and st=1 in equilibrium
must also be bounded
away from zero and infinity, since ct=yt and st=1 in equilibrium
- second, notice that the term
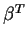 goes to zero as T goes to infinity
goes to zero as T goes to infinity
- this implies that, as long as qt+T does not explode towards infinity, the
transversality condition must hold
- can we have an equilibrium in which qt+T explodes towards infinity? No,
because the agents' wealth in terms of the quantity of durable
good they possess would also be shooting up to infinity, and it would be optimal
for the agent to sell some of the durables they possess and try to increase their
consumption of the non durable good
What did we learn so far?
- the value of an asset (durable) good is the price of the asset (durable) expressed
in terms of the consumption good. we will think of the price level as reflecting
the value of money in terms of the consumption good.
- people are forward looking, in the sense that the price of an asset and of
a durable good depend on the expectations about, respectively, the future dividends
generated by the asset and the services obtained from the durable good. in the remainder
of the course we will show that this is true for money as well: the current price
level depends on the future services generated by holding money balance.
references: Milton Friedman, The Optimal Quantity of Money and Other Essays,
Chicago, Aldine, 1969



Next: About this document ...
Marco Del Negro
2000-01-18