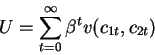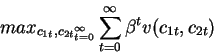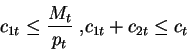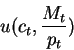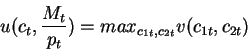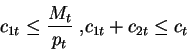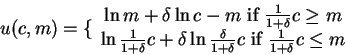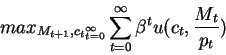Next: About this document ...
CLASS 3: THE ROLE OF MONEY: A ``CASH IN ADVANCE创 MODEL
- What is money?
- Why do people hold money?
- A formal model of why people hold money: a ``cash in advance创 model
What is money, and why do we use it?
Example: cigarettes as money in WWII Prisoner-of-War camps.
Money as a device for making transactions.
Barter economy is inefficient because of: 1) search costs
2) lack of specialization
Why cigarettes. Cigarettes satisfy a number of criteria for being
``good money":
- cigarettes are portable, and ``divisible" - an individual cigarette
has small enough value (medium of exchange)
- a cigarette is a fairly standardized commodity, whose value in terms
of other goods is easy to ascertain (unit of value)
- cigarettes do not spoil quickly (store of value)
but cigarettes (like gold) have an alternative use - resource cost
What is money for?
- Money as a medium of exchange for transactions:
money makes trade less costly
- Money as unit of value:
makes the value of other commodities or services easy to ascertain...
when the ``real value" of money is not uncertain
in countries with hyperinflation money prices are changed frequently and
unpredictably: money, while still sometimes used as medium of exchange, is
no longer used as unit of account (instead, dollars are used;
Chile: ``unidad de fomento", Mexico: UDI(?))
- Money as store of value:
money as an asset: keep your savings under the mattress
(why is it inefficient?)
The Monetary Aggregates
Assets differ in their ``moneyness", that is, in their ability to
``substitute" currency as a medium of exchange (and unit of value)
- M1: currency, checkable deposits (travelers' checks)
most liquid (you can pay with checks... almost all the time)
- M2: M1 + savings deposits, time-deposits (1 day, 28 days), money
market mutual funds
less liquid (wait time, cannot write checks for less than...)
changes in monetary aggregate due to ATM machines
- M3 and L: M2 + short term assets (treasury bill, commercial paper)
``liquidity": readily exchangeable, small default risk, etc.
what is the relevant monetary aggregate?
The Cash-in-Advance Model
In the rest of the course we will simply assume that money enters in
the utility function of agents. In particular, we
will study objective function of the type:
(note the similarity with the model for durable goods)
however, in the remainder of this class we will see that such a utility function
can be derived from a model which has some features that recall some of the ideas
discussed in the first part of this class, and in particular the fact
that people need to use cash in order to purchase some
kinds of goods (for example, a cappuccino)
Try to model an ``exchange technology创 which justifies why people use money.
The idea is that there are credit goods (say, a car), which can
be purchased using credit (say, American Express), and cash goods, which
have to be purchased using money.
reference: Clower, R.W.,1967, ``A reconsideration of the Microfoundations of
Monetary Theory,创 Western Economic Journal,6, pp. 1-9
Lucas, Robert E. Jr., and Nancy L. Stokey, 1987, ``Money and Interest in a
Cash-in-Advance Economy创, Econometrica, Vol.55, pp. 491-513
Assumptions
- at the beginning of each period t the household has a quantity of
money Mt inherited from the previous period, and receives an endowment
yt
- the households enjoys consuming both cash and credit goods (which are not
perfect substitutes). its objective is to maximize the utility function:
- there is specialization within the household. One member of the
household (say, the wife) is the seller: she stays in the shop and sells
the endowment yt. Another member of the household (say, the husband)
is the buyer: he goes to the market and buys both cash and credit goods
- cash and credit goods have the same price expressed in monetary terms: pt.
This is because the two goods are perfect substitutes in production, in the sense
that the seller can divide the endowment yt into
cash goods (y1t) and credit goods (y2t) subject to the constraint:
- the seller sells cash goods obtaining cash, and credit goods obtaining credit,
which will be settled at the end of the day
- in the meanwhile, the buyer is buying at the market both cash (c1t)
and credit goods (c2t). A crucial feature of the model
is that the buyer can buy cash goods only using the money Mt held at the beginning
of period t. In other words, there is a cash in advance constraint:
the credit good can be purchased for credit, which again will be settled at
the end of the day
- at the end of the day all credit transactions are settled, and the budget
constraint for the household is:
or
where the first term is cash left from the buyer, the second is cash
obtained from selling cash goods, and the last term is the settlement of
credit transactions
wrapping up, the household's problem is:
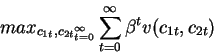
subject to:
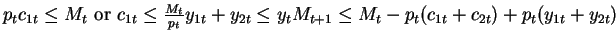
now, notice that the amount of money the household saves for
next period depends only on total consumption, and not on
the division between cash and credit goods. that is, if we call
ct=c1t+c2t
the intertemporal budget constraint becomes:
We can divide the household's problem in two steps, an
intratemporal problem and an intertemporal problem:
Step 1 (intratemporal):
Given the initial quantity of money Mt and the price level pt,
and for a given choice of ct (which in turn determines
next period's money Mt+1
through the budget constraint), the household decides how to split
consumption between cash and credit goods. The problem is then:
maxc<<86>>1t,c<<87>>2t v(c1t,c2t)
subject to
notice that the solution to this problem is a function of the
two variables determining the constraints, namely ct and
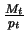 .
we can then define an indirect utility function,
.
we can then define an indirect utility function,
which is defined as:
subject to
The following example may clarify things a little:
say that
(notice we can drop the time index because we are studying the intratemporal
problem)
call
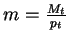
the problem is:
subject to
how do we solve this problem? we ignore the first constraint (for the time
being) and we substitute the second constraint in the objective function:
and obtain the solution:
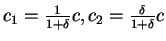
if
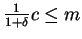 (that is, the cash in advance constraint is
not binding), then this is the solution of the problem. Otherwise, the solution is:
(that is, the cash in advance constraint is
not binding), then this is the solution of the problem. Otherwise, the solution is:
c1=m,c2=c-m
so that the indirect utility function is:
Step 2 (intertemporal): give the indirect utility function, the consumer
chooses the total consumption ct and the money balances Mt that solve:
subject to
and for given M0
In the remainder of the course we will forget about cash and credit goods,
and work only with the indirect utility function. However, the payoff from
doing all this math is that we know why real money balances enter in the
utility function.
What did we learn?
- we discussed the 3 roles of money (unit of account, store of value,
medium of exchange)
- we studied a model (Cash-in-Advance Model) where money is needed by the
household as a medium of exchange in order to buy some kinds of goods
(``cash goods创)
but it is also store of value and unit of account!
- derived an indirect utility function which we are going to use in the
rest of the class



Next: About this document ...
Marco Del Negro
2000-01-24